Eine eigene Formelsammlung anzulegen kann viel Arbeit bedeuten. Wie du dennoch eine für dich funktionierende Sammlung anlegen kannst und gleichzeitig effizient vorgehst, erfährst du hier.
Zu Beginn vieler Veranstaltungen wird festgelegt, dass du für die Klausur eine eigene Formelsammlung mitnehmen darfst. Häufig wurden bereits solche Sammlungen in den Vorjahren entweder von den Dozenten selber oder von Kommiliton/innen zusammengestellt. Im ersten Moment erscheint es ziemlich praktisch, sich einfach die Formelsammlung herunterzuladen und auszudrucken, jedoch kann die Arbeit mit solchen Sammlungen auch schnell schwierig werden. Es kann hilfreich sein, diese Formelsammlungen viel mehr als Startpunkt für deine Eigene zu sehen.
Suche dir zuerst heraus, was deine Formelsammlung beinhalten darf, z.B. darf die Formelsammlung nur aus den Formeln und Überschriften zu den einzelnen Kapiteln bestehen, oder darfst du auch Kommentare reinschreiben? Manchmal werden Formelsammlungen vor der Klausur von Tutoren kontrolliert, weshalb du darauf achten solltest mögliche Vorgaben einzuhalten. Wir haben dir eine Liste mit Problemen und Lösungsansätzen zusammengestellt, mit deren Hilfe du eine Formelsammlung erstellen kannst, die auf deine Bedürfnisse zugeschnitten ist.



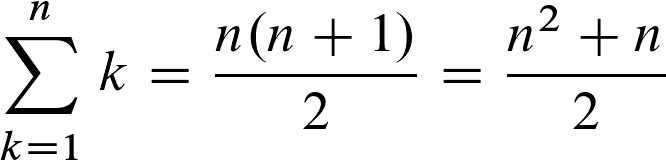
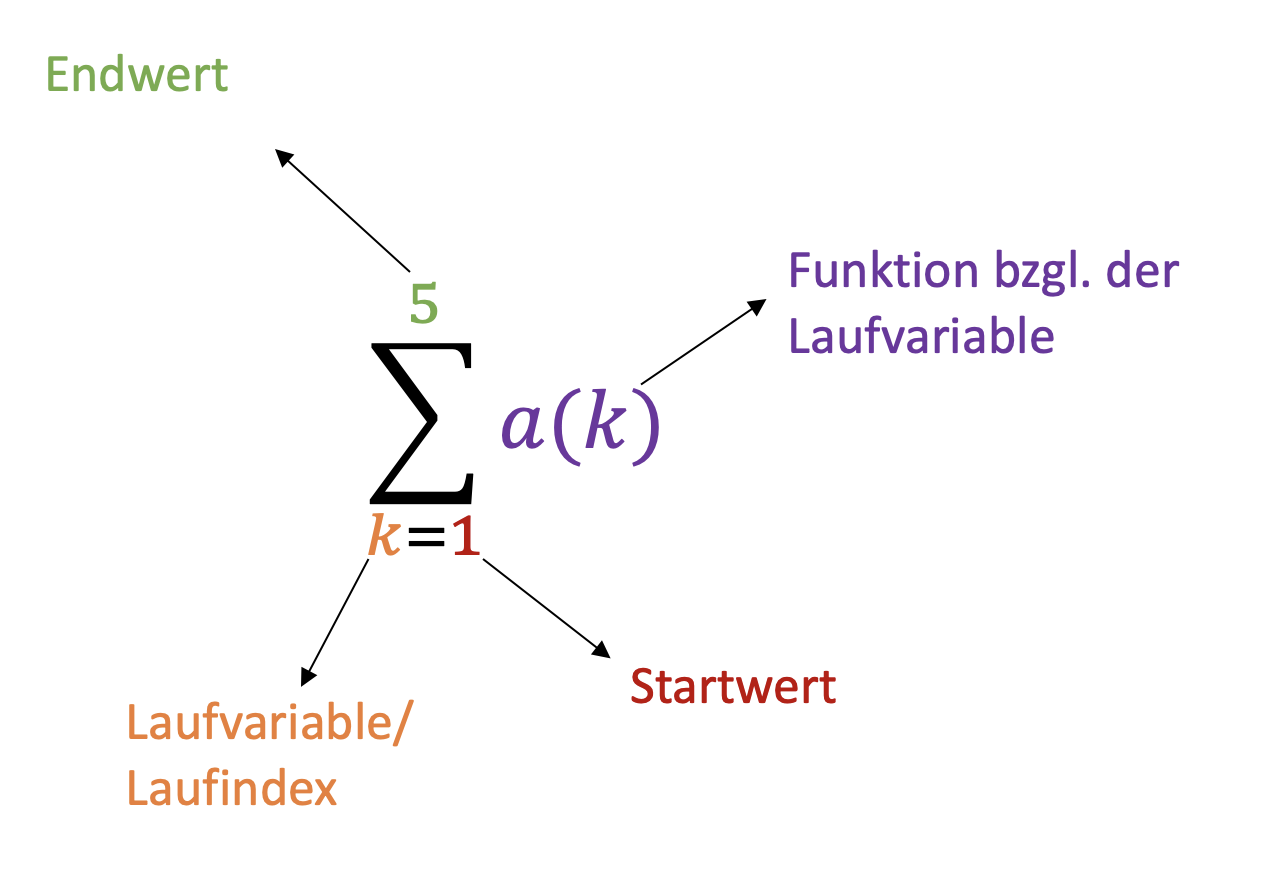
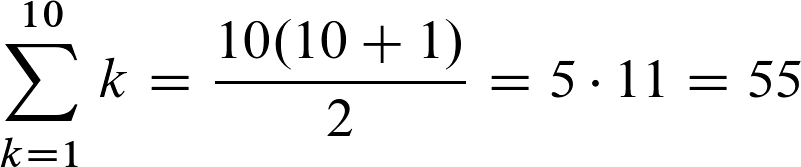
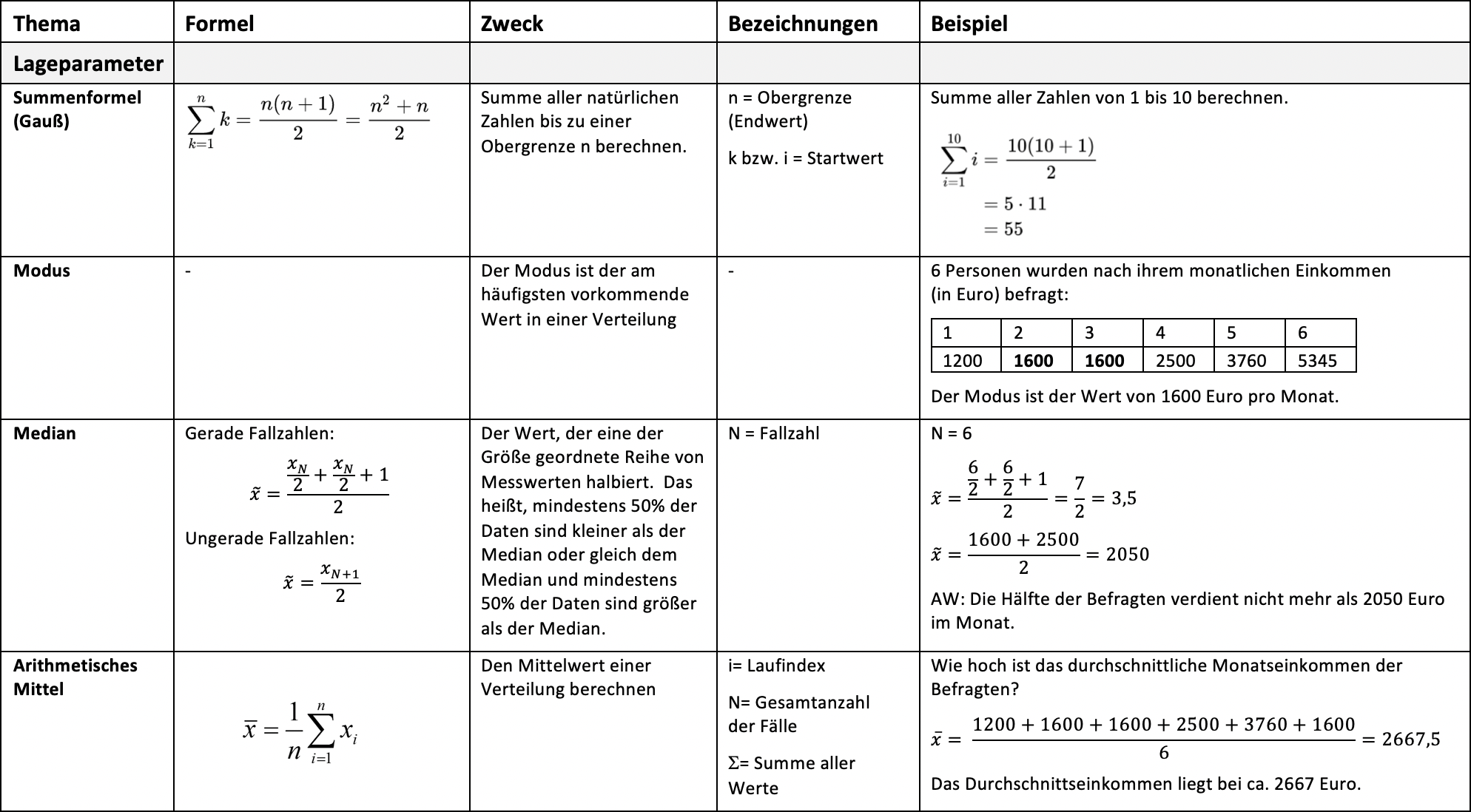



Schreibe einen Kommentar