Aller Anfang ist schwer. Gerade die Mathematik im ersten Semester kann sehr überwältigend sein: Vorlesung, Übung, Tutorium sowie Übungsaufgaben, die jede Woche bearbeitet werden müssen. Um Zeit und Arbeit zu sparen, empfehlen wir dir, die Aufgaben in einer Gruppe zu bearbeiten. Doch wie gestaltet man die Zusammenarbeit möglichst effektiv?
Aufbau der Veranstaltung
Sehen wir uns zunächst einmal an, wie die Veranstaltung aufgebaut ist. Starte dazu unser kleines Video.
Arbeit in den Übungsgruppen
Es gibt Arbeitsgruppen, die gut funktionieren und andere, die man als zusätzliche Last erlebt. Damit das nicht passiert, haben wir ein paar Empfehlungen zusammengestellt, wie man effizient in Übungsgruppen arbeitet.
Wer mit wem?
Bevor ihr loslegen könnt, müsst ihr euch als Team finden. Im ersten Semester gehen die meisten recht pragmatisch vor und verabreden sich mit denjenigen, die neben ihnen in der Vorlesung sitzen. Habt ihr eure Kontaktdaten ausgetauscht, solltet ihr nicht einfach loslegen, sondern den Rahmen klären, d.h. wie ihr euch die Zusammenarbeit vorstellt. Ansonsten kann es schnell passieren, dass die Gruppe zerbricht, weil alle unterschiedliche Erwartungen hatten, die nie auf den Tisch kamen.
Ein Vorschlag für den Ablauf in den Gruppen
Meist spielt sich im Verlauf des Semester eine Routine ein, in der man zusammenarbeitet. Wir empfehlen Euch wie folgt vorzugehen. Klicke auf die Plus-Buttons, um mehr zu erfahren.
Hier noch einmal alle Punkte im Detail:
Manche Gruppen laufen wie folgt ab: ein Teil bereitet sich vor, ein Teil nicht. Manchmal gibt es auch jemanden, der die Aufgaben schnell durchrechnet und keiner kommt so richtig mit. Das spart vielleicht Zeit, aber rächt sich doppelt bei der Klausurvorbereitung.
Wir empfehlen euch, dass jeder sich vor dem Treffen Gedanken zu den Aufgaben macht. Das bedeutet nicht, dass ihr alle Aufgaben schon im Voraus rechnen müsst. Geht stattdessen ein paar grundsätzliche Fragen durch:
- Worum geht es?
- Was ist genau gefragt?
- Wie würde ich vorgehen?
- Wie würde ich das rechnen?
Haltet eure Lösungsansätze schriftlich fest. Hier zwei Beispiele für Notizen zur Vorbereitung eines Übungsgruppentreffens.
So gelangt ihr zu einem Lösungsansatz, der euch nicht nur das Verständnis erleichtert, sondern auch bei der Klausurvorbereitung unterstützt. Ihr könnt dann schneller bestimmte Aufgabentypen identifizieren und habt direkt einen Lösungsweg für diese parat.
Sollte die Zeit, gerade vor der Klausur einmal zu knapp werden, teilt euch bei den Lösungsansätzen auf. Seid ihr zu dritt und habt sechs Aufgaben, würde in diesem Fall jeder zwei Lösungsansätze vorbereiten und mitbringen. Sammelt auch Verständnisfragen zur Vorlesung oder markiert euch Formulierungen, die ihr nicht verstanden habt.

Kennst du die genervten Blicke, wenn jemand immer wieder Fragen stellt, die sich auf die Grundlagen beziehen, aber nicht auf die Übungsaufgaben? Es ist normal, dass einige Fragen zur Vorlesung oder zum Stoff haben. Damit ihr trotzdem genug Zeit für die Übungsaufgaben habt, empfehlen wir, dass diejenigen, die Fragen zu Vorlesung haben, das vorab besprechen – oder, falls es alle betrifft – zu Beginn eures Treffens klären.
Einige nutzen dafür Chat-Gruppen, in denen sie Links zu hilfreichen Erläuterungen oder Erkärvideos austauschen. Anderen ist es lieber, sich vorab zu treffen – zum Beispiel direkt vor dem Übungsgruppentreffen.
Lösungsansätze vergleichen
Vergleicht eure Lösungsansätze und einigt euch auf einen. Diese Diskussion ist wichtig, um euer Matheverständnis zu stärken und macht euch selbstsicherer beim Vorrechnen in den Übungen.
Gemeinsam berechnen und visualisieren
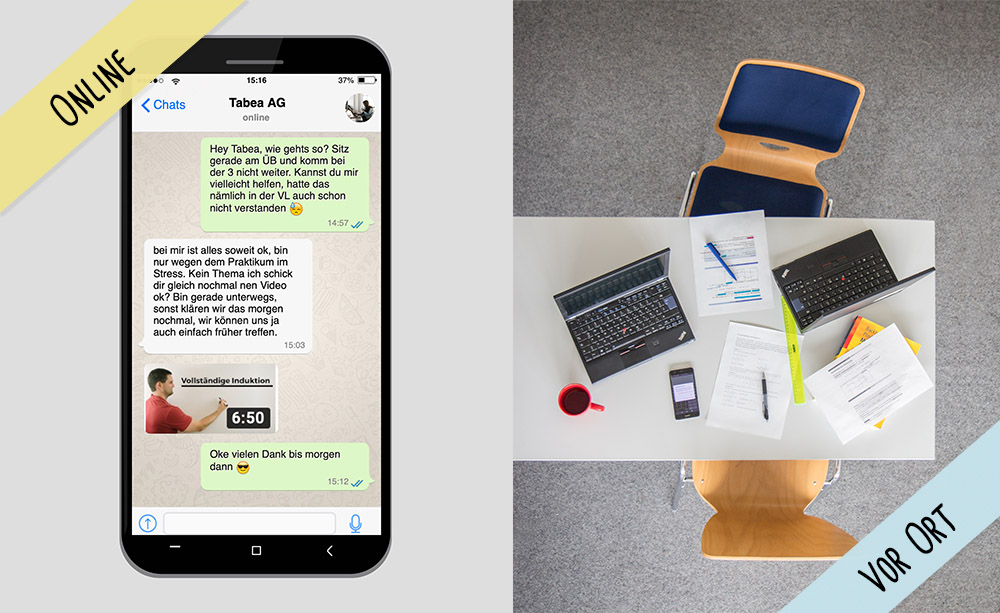
Jetzt geht’s an die eigentliche Arbeit: das Rechnen. Achtet darauf, dass jeder mitkommt. Falls ihr selbst nicht mitkommen solltet, sprecht es an. Es bringt nichts Lösungen abzugeben, die ihr nicht versteht! Es lohnt sich, wenn eine/r den Lösungsweg für alle festhält und kommentiert. So versteht ihr auch im Nachhinein, wie und warum ihr zu welchem Ergebnis gekommen seid. Auf diese Weise könnt ihr leichter die Fehlerquellen identifizieren und korrigieren, falls ihr doch mal falsch gerechnet haben solltet. Entscheidet euch, ob ihr das Treffen online durchführt, z.B. per Skype oder Discord, oder ob ihr euch vor Ort trefft. Probiert es aus und findet die für euch passende Form der Zusammenarbeit!
Im besten Fall habt ihr euch vorab geeinigt, wer während des Treffens eure abgabefertige Lösung inklusive der Kommentare erstellt und diese an die anderen Gruppenmitglieder weiterleitet. Wir empfehlen euch dafür einen Latex-Editor zu nutzen. Diese Musterlösung wurde mit dem Latex-Editor „Overleaf“ erstellt. Die Kommentare sind ebenfalls direkt in dem Code erstellt worden. Mehr dazu findest du in unserem Tutorial Arbeiten mit Latex.

Source-Code für Kommentare mit Overleaf:
\usepackage[draft]{todonotes}\intertext{\todo [inline]{Kommentar}}
Beispiele für die Ausgabe:
Hat sich doch ein Fehler in eure Lösung eingeschlichen, ärgert euch nicht, sondern verbessert diese in den Musterlösungen! Hinterlasst eine Notiz, warum der ursprüngliche Weg falsch war und wie man zum richtigen Ergebnis kommt. So seid ihr auf jeden Fall auf dem richtigen Weg zu einem besseren Matheverständnis und legt wichtige Grundsteine nicht nur für die Klausur, sondern auch für euer weiteres Studium.
Und wie bereitet man sich auf die Klausur vor? Mehr Tipps findest du z.B. hier: Prüfungsstrategie Mathematik I


Schreibe einen Kommentar