Du willst stressfrei für eine Matheklausur lernen? Das scheint zunächst unmöglich, aber mit den richtigen Routinen und einem guten Masterplan kannst Du es schaffen.
Mathematik Grundlagenvorlesungen sind ein wichtiger Bestandteil vieler Studiengänge. Die abstrakten Inhalte, das hohe Lerntempo und der nicht immer auf den ersten Blick erkennbare Zusammenhang zum eigenen Fach kann einem das Leben schwer machen. Wir haben Studierende nach den zentralen Herausforderungen in der Mathematik I gefragt und in einer Mindmap zusammengestellt.
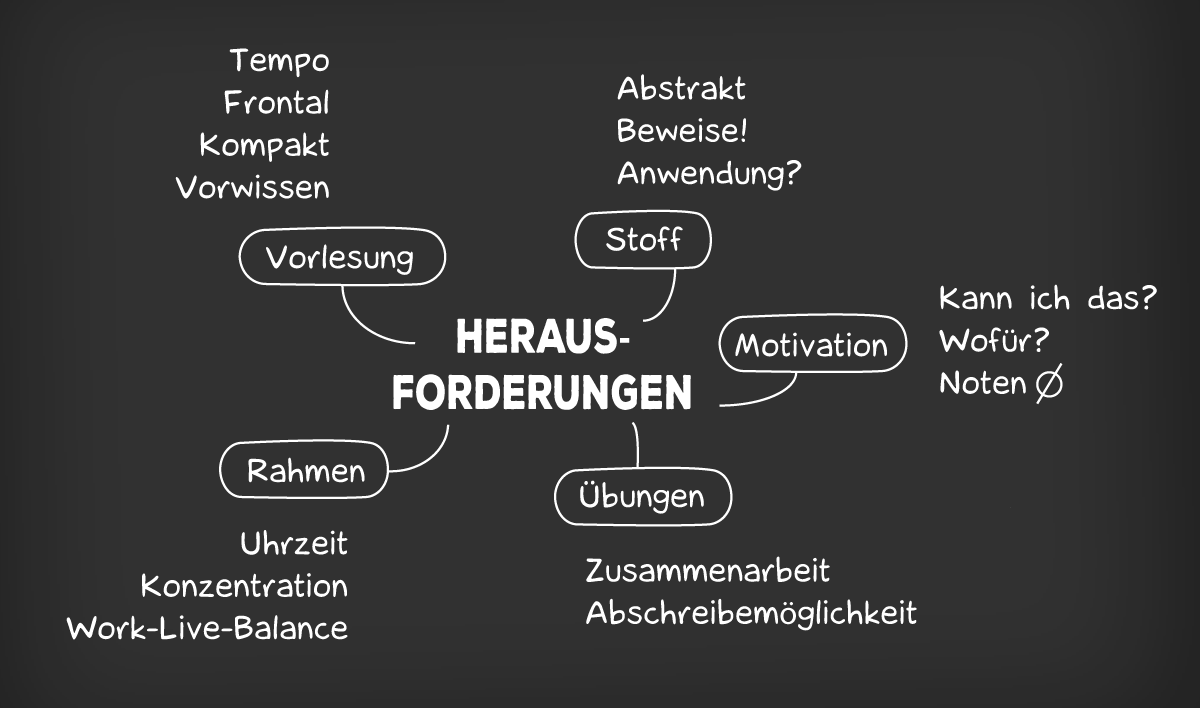
Das Tempo in der Vorlesung kann einen an die eigenen Grenzen bringen, da die PowerPoint-Folien i.d.R. zügig besprochen werden. Daher ist es wichtig, gut vorbereitet zu sein und sich vorab genau zu überlegen, wie man sich in der Vorlesung verhält.
Um die Inhalte wirklich verstehen zu können, müssen die Grundlagen sitzen. Wir eine Routine aussehen kann, erfährst du im Film.
Lernangebote:
- MintFITOnline-Test, um die eigenen Mathematikkenntnisse zu überprüfen
- Vorkurse Mathematik (Präsenz) Freiweilliger Vorkurs des Fachbereichs Mathematik für alle Studierende der Bachelor- und Lehramtsstudiengänge
- OBM+Online Mathematik Brückenkurs
- ViaMINT Videobasierte interaktive Vorkurse
Das Tempo in der Mathematik-Vorlesung ist im Vergleich zum Schulunterricht relativ hoch. In der Mathematik I und II werden z.Z. v.a. Folien präsentiert, in der Mathematik III und IV erläutern viele Dozent/innen den Stoff an der Tafel. Gehen wir zunächst einmal von einer Stoffvermittlung per Folie aus.
Drucken oder Download
Häufig stellen die Lehrenden die Folien kurz vor der Vorlesung online zum Download. Wir empfehlen dir, die Folien vor der jeweiligen Vorlesung auszudrucken oder sie auf ein Tablet oder Laptop mit Touchscreen und Stifteingabe herunterzuladen, sodass du deine Notizen direkt auf die Folien schreiben kannst. Dazu eignet sich bspw. das kostenlose Microsoft OneNote 2016.
Minimalnotizen
Ergänze das Wichtigste in kurzen Stichpunkten, sodass du nicht hinter dem Tempo des Vortrags zurückfällst. Das können z.B. Rechenschritt sein, die von den Dozenten erläutert, jedoch nicht auf den Folien beschrieben werden. Es wichtiger, den Gedankengang folgen zu können, als alles niederzuschreiben.Grundsätzlich helfen dir die Fragen:
- Worum geht es gerade?
- Wie lautet das Kernproblem?
- Womit wird was bewiesen?
Ergänze deine Notizen durch eigene Gedanken und Fragen.
Icons nutzen
Nutze Icons, um Verständnisschwierigkeiten, Exkurse, Beispiele oder wichtige Hinweise der Dozenten zu dokumentieren. Arbeitest du mit gedruckten Folien eigenen sich Post-It-Marker bzw. Lesezeichen. Nutze die unterschiedliche Farben für verschiedene Zwecke, wie „Verständnisproblem“ oder „wichtiges Beispiel“.
Mehr Tipps zur Arbeit mit Icons findest Du hier: Besseres Leseverständnis mit einem ICON Set.
Nachfragen sind erlaubt!
Frage die Dozenten in der Vorlesung oder die Tutoren in der Übung, falls Du etwas nicht verstanden hast! Viele trauen sich nicht, vor der Gruppe Fragen zu stellen. Die Dozenten denken, jeder hätte es verstanden und fahren mit dem Stoff fort. Davon hat niemand etwas – meist sind die anderem einem dankbar, wenn jemand nachhakt. Nur weil keiner fragt heißt das nicht, dass alle außer dir den Stoff verstanden hätten 😉
Gute Foliennotizen erstellen
Was meinst Du, welche Form von Foliennotizen ist gelungen? Wir haben drei Beispiele zusammengestellt. Welche ist die gelungenste Annotation?
Tafelanschrieb: Im Tandem arbeiten!
In Mathematik III und IV werden die Inhalte i.d.R. an die Tafel geschrieben. Daher eignet sich hier ein anderes Vorgehen. Wir empfehlen dir die Arbeit aufzuteilen: eine/r schreibt mit, der/die andere hört vor allem zu und überarbeitet im Nachhinein ggf. die Mitschrift.

Die beste Vorbereitung ist die Nachbereitung. Wenn du dich effektiv auf die nächste Vorlesung vorbereiten möchtest, solltest du dir nochmal ansiehst, was ihr in der letzten Stunde besprochen habt.
- Inhalte im Kopf durchgehen: Lehne dich zurück, schließe die Augen und versuche, dich an das Wichtigste zu erinnern.
- Marker sichten und Wissenslücken schließen: Sieh dir die annotieren Folien an, auf denen Du Verständnisschwierigkeiten oder Fragen markiert hattest (z.B. mit den Icons oder Klebezetteln)Beispiel: bijektive AbbildungenSuche Dir ggf. zusätzliche Erklärungen suchen. Sollten sich die Lücken auf Grundlagenwissen beziehen, empfehlen wir Dir die Plattformen OBM+ und ViaMINT. Geht es um neue Methoden und Modelle, musst du etwas kreativier werden. Vielleicht findest Du eine gute Erklärung in einem Youtube-Kanal (TheSimpleMaths, DorFuchs, Khan Academy, brainfaqk u.a.)Weitere Tipps und Tricks fürs Mathe lernen, findest du in den Tutorials „Wie lernt man mathematische Beweisführung?“ und „Beweisführung am Beispiel“.

- Zusammenfassung erstellen: Halte Deine Zusammenfassung möglichst direkt im Anschluss fest – z.B. mit Onenote.

- Folien durcharbeiten: In dem Handout von Janko Latschev findest du gute Reflexionsfragen für das Durcharbeiten der Vorlesung. Markiere dir insbesondere die Abschnitte, die im Skript mit Erläuterungstexten versehen sind. Du kannst davon ausgehen, dass diese Inhalte wichtig für die Klausur sind.
- Lernstands-Mindmap: Wir empfehlen dir, eine Mindmap zu den Themen der Vorlesung zu suchen oder selbst eine zu erstellen. Auf der Mindmap kannst Du markieren, welche Themen du schon gut kannst, und welche noch nicht. Das geht z.B. gut mit dem Programm XMind (Windows & MacOS).
Mittwoch, 8:45, Mathe-Vorlesung: es gelingt dir kaum noch die Augen offen zu halten, geschweige denn zuzuhören? Mit folgenden unauffälligen Tricks kannst du die Zusammenarbeit deiner beiden Gehirnhälften wieder in Schwung zu bekommen und auf die Weise deine Aufnahmefähigkeit und dein Leistungsvermögen steigern.
Das Tempo in der Vorlesung kann einen an die eigenen Grenzen bringen, da die PowerPoint-Folien i.d.R. zügig besprochen werden. Daher ist es wichtig, gut vorbereitet zu sein und sich vorab genau zu überlegen, wie man sich in der Vorlesung verhält.
Mathematik kann man lernen
Nur weil du nicht verstanden hast, was in der letzten Vorlesung besprochen wurde, heißt das nicht, dass du dein Studienfach wechseln musst. Überzeugungen wie „Ich verstehe Mathe einfach nicht.“ oder „Ich kann das nicht.“ sind aus zwei Gründen ungünstig:
- Sie suggerieren, dass man prinzipiell nicht geeignet sei (Generalisierung) und verknüpfen in unzulässiger Weise „fehlendes Wissen“ mit allgemeinen Persönlichkeitseigenschaften wie der generellen Auffassungsgabe.
- Sie bieten eine scheinbare „einfache“ Erklärung für ein Problem („Ich kann es ja nicht besser.“) und verführen dazu, in Passivität zu verharren, anstatt nach Lösungen zu suchen.

Sollte es dir ähnlich gehen, empfehlen wir dir, sich in solchen Momenten innerlich ein kleines „Stoppschild“ vorzustellen und dir zu sagen, dass diese Art von Gedanken nicht hilfreich sind. Versuche stattdessen:
- Dir bewusst zu machen, dass nur weil du ein Thema nicht verstanden hast, nicht generell unbegabt bist, sondern sich die meisten Themen mit etwas Ruhe und Sorgfalt auch im Nachhinein erschließen lassen. Eine Langzeitstudie mit 3500 bayerischen Schülern hat gezeigt, dass Intelligenz nur in jungen Jahren eine Rolle spielt. Viel entscheidender sind die Motivation und die Lernstrategie (Murayama, 2013).
- In Lösungsoptionen zu denken, anstatt sich selbst abzuwerten. Vielleicht sagst du dir „Okay, das habe ich nicht verstanden – was kann ich tun?“.
- Z.B. andere Erklärungen suchen?
- Übungsaufgaben suchen?
- Mit Kommilitonen sprechen?
- Die Aufgabe in kleine Häppchen aufteilen? (Formeln finden, Größen identifizieren, usw.).
- Versuchen die Aufgabe, anders zu lösen – z.B. geometrisch?
Wenn man eine Sprache erlernen will, fällt das den meisten auch nicht einfach zu, sondern man muss Vokalen einüben und sich mit Grammatikregeln auseinandersetzen. Das gleiche gilt auch für die Mathematik.
Informiere dich über das „warum“
Die Frage nach dem „Warum“ ist verständlich. Vor allem im ersten Semester fällt es schwer, den Zusammenhang zu den Inhalten des eigenen Fachs herzustellen – es sei denn du studierst Mathematik im Hauptfach. 🙂
In der Biochemie benötigt man bspw. die lineare Algebra, um für Patienten notwendige Dosierungen von Medikamenten zu berechnen. Mit diesen Berechnungen wirst du vielleicht erst im Biochemie-Master konfrontiert, dennoch ist es hilfreich, sich bereits jetzt vor Augen zu führen, inwiefern die Mathematik für dein Studium sowie deinen späteren Beruf relevant ist. Sprich im Zweifelsfall mit Kommiliton/innen höherer Semester oder Lehrenden bzw. Tutoren, um die Zusammenhänge und Anwendungsbezüge zu verstehen.
Lass dich nicht beirren
„Also ich habe gehört, dass hier im Schnitt 80 % durchfallen. Das ist pures Glück, wenn man besteht.“
„Hast Du dich auch mit der linearen Regression beschäftigt? Ich glaube, dass hatte sie mal in der Vorlesung erwähnt.“
Du kennst das sicher: vor einer Klausur kochen die Gerüchte hoch und ein jeder meint, von neuen Schreckensnachrichten zu berichten. Lass dich von Gerüchten und destruktiven Aussagen anderer nicht beirren. Frage ggf. nach, auf welchen Fakten diese Aussagen berufen. Oft stammen die Informationen aus vorherigen Jahrgängen. Prüfungen und Dozenten ändern sich jedoch mit der Zeit und damit auch die Anforderungen. Es lohnt sich nicht, sich die eigene Laune und Motivation durch vage Aussagen anderen verderben zu lassen. Widmest du dich dem Thema zuversichtlich und optimistisch, wird sich das auch positiv auf dein Lernergebnis auswirken. 🙂
Hier findest du noch einmal alle wichtigen Etappen bis zur Klausur im Überblick:

Und falls dich das Thema „Beweise“ umtreibt, dann schau dir doch einmal unsere Erklärfilme dazu an: Mathematische Beweisführung lernen
Literatur
Murayama, K., Pekrun, R., Lichtenfeld, S. & vom Hofe, R. (2013). Predicting Long-Term Growth in Students‘ Mathematics Achievement: The Unique Contributions of Motivation and Cognitive Strategies. Child Development 84(4): 1475-1490.
https://srcd.onlinelibrary.wiley.com/doi/full/10.1111/cdev.12036


Schreibe einen Kommentar