In Physikalische Chemie 1 & 2 gibt es einige Besonderheiten bei den Vorlesungen, Übungen und der Klausur. Damit du dich trotz vieler Tafelbilder und schwierigen Übungen gut auf die Klausur vorbereiten kannst, haben wir dir einige Tipps zusammengestellt.
Allgemeine Tipps
Wie kommst du gut in der Vorlesung mit? Wie bereitet man sich auf die Übung vor und wie auf die Klausur? Hier unsere Empfehlungen:
Schon am 1. Termin wirst du bemerken, dass die Vorlesungen in Physikalischer Chemie etwas anders ablaufen, als andere Vorlesungen, die du bereits kennst. Wie du trotzdem gut mit den verschiedenen Herausforderungen umgehen kannst, erklären wir dir jetzt:
Umgang mit den Folien
In der Vorlesung werden sowohl Folien präsentiert als auch mit der Tafel gearbeitet. Der Stoff auf den Folien ist teilweise sehr verdichtet und komplex. Zum Teil werden digitale Texte mit Zeichnungen kombiniert. Die Herausforderung besteht darin, zu verstehen, welche Abläufe auf den Folien beschrieben werden und wie die Graphen und Formeln zu verstehen sind. Hier zwei Beispiele, wie Folien aussehen können:
Michaelis Menten Enzymkinetik:
![]()
![]()
![]()
![]()
![]()
![]()
Prinzip der Quasistationarität:
Näherung: Konzentration der Zwischenprodukte bleibt nach der Induktionsphase konstant.
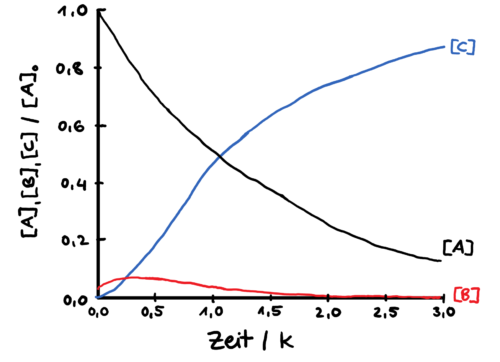
![]() ist klein und konstant
ist klein und konstant
![]()
![]() Anscheinend entsteht C direkt aus A mit langsamster Geschwindigkeitskonstante
Anscheinend entsteht C direkt aus A mit langsamster Geschwindigkeitskonstante ![]() nach 1. Ordnung.
nach 1. Ordnung.
![]() .
.
Unsere Tipps:
Als erstes raten wir dir, dich möglichst weit nach vorne zu setzen, um die Werte auf den Folien gut erkennen zu können. Falls möglich, lade dir die Inhalte vorab auf einen Laptop/Tablet/eBook-Reader oder Smartphone.
Versuche, die Erläuterungen direkt in der Vorlesung nachzuvollziehen und arbeite lieber sparsam mit Notizen. Wir empfehlen dir, dass du die Folien zeitnah nach der Vorlesung noch einmal durchgehst und dir (zusätzliche) Notizen machst.
- Erstelle kleine Zusammenfassungen der Vorlesungsinhalte (max. 2 – 3 Sätze zu jeder Folie) Hier ein Beispiel zum Thema Katalyse. Du kannst die Mini-Zusammenfassung später zu Karteikarten für die Klausurvorbereitung ausbauen

- Erstelle dir eigene Abbildungen und Diagramme. Auf diese Weise kannst du die Inhalte besser nachvollziehen und hast bereits einen Teil der Klausurvorbereitung erledigt.
Für 6 – 7 Folien kannst Du ca. 30 – 60 Minuten für die Nachbereitung einplanen.
Umgang mit dem Tafelanschrieb
Ein Großteil des Stoffs wird in der Physikalischen Chemie über Tafelanschriften vermittelt. Das zeitgleiche Verstehen und Mitschreiben ist oft nicht ganz einfach, vor allem wenn die Dozenten sehr schnell schreiben und währenddessen die Inhalte erläutern. Viele stehen vor der Frage, ob sie das Tafelbild abschreiben sollen oder doch am Ende ein Foto aufnehmen und während der Vorlesung lieber zuhören.
Eine Möglichkeit besteht darin, dich mit einem Kommilitonen / einer Kommilitonin zusammen zu tun und als „Tandem“ zu arbeiten. Dabei schreibt einer alles mit, was an die Tafel geschrieben wird, der andere hört zu und ergänzt gegebenenfalls die Notizen des Mitschreibers. Direkt nach der Vorlesung könnt ihr euch austauschen und durchgehen, ob ihr alles verstanden und aufgeschrieben habt.
Hier ein Beispiel einer Mitschrift:
Falls es doch mal viel zu schnell geht, könnt ihr zwischendurch bzw. am Ende Fotos von der Tafel machen und eure Notizen später ergänzen. Das kann allerdings schwierig sein für den Fall, dass das Bild nicht sehr scharf ist und man die Formeln nachträglich entziffern muss.
Sieh dir direkt nach der Vorlesung nochmals die eigene Mitschrift an, um zu überprüfen, ob du auch alles verstanden hast.
Sollten für dich noch Fragen offenbleiben, wende dich am besten an deine Kommilitonen/innen oder deinen Professor/in – sowohl während als auch nach der Vorlesung. Nutze ggf. zusätzlich Erklärvideos, um die Inhalte besser nachvollziehen zu können, z.B. bei
In den Übungen werden Aufgaben besprochen, die nach der Vorlesung zur Verfügung gestellt werden. In der Klausur werden dir ähnliche Aufgaben gestellt, daher ist es sehr wichtig, die Übungsaufgaben zu verstehen und selbst lösen zu können.
In der Übung stellen die Teilnehmer/innen ihre Lösungen vor und werden ggf. durch den Dozenten / die Dozentin korrigiert. Das kann schwierig werden, für den Fall, dass der Student / die Studentin sich nicht vorbereitet hat und so oft korrigiert werden muss, sodass man den Überblick über den richtigen Lösungsweg verliert. Auch werden in der Vorlesung nicht immer alle für die Übungsaufgaben relevanten Formeln vermittelt.
Daher empfehlen wir dir:
- Bereite, dich in einer Übungsgruppe vor, um die Musterlösungen besser nachvollziehen zu können. Eine Größe von 2 – 3 Teilnehmern/innen sind optimal für die Zusammenarbeit.
- Suche die benötigen Formeln vor dem Treffen in der Übungsgruppe selbst heraus bzw. versuche bekannte Formeln umzuformen. Alternativ kannst Du auch im Internet nach dem Namen der Formel suchen, z.B. nach der „Freien Mischungsenthalpie“ und überlegen, ob dir diese bei der Aufgabe weiterhelfen.
- Erarbeitet euch im Nachhinein, also nach der Übung, am besten eine Musterlösung. Diese könnt ihr gut bei der Klausurvorbereitung nutzen. Ein allgemeines Vorgehen für die Bearbeitung der Aufgaben findest Du am Ende dieses Tutorial.
Mehr Tipps zur Organisation der Gruppen findest Du hier:
Übungsaufgaben effektiv in Gruppen bearbeiten
In dem Modul Physikalische Chemie (PC) besteht die Klausur aus Aufgaben, die den Übungen sehr ähneln. Sowohl in PC 1 als auch in PC 2 hat man 90 Minuten Zeit für die Bearbeitung der Aufgaben.
Wie ist die Klausur aufgebaut?
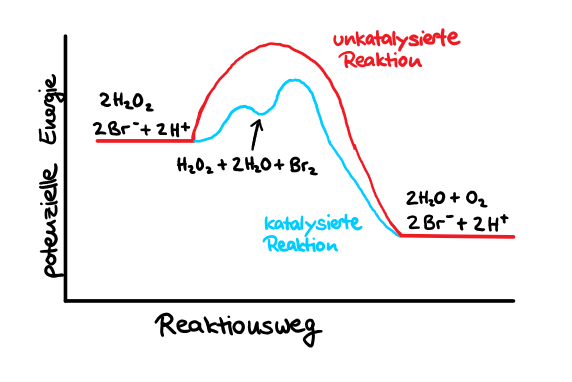
In PC 1 musst du chemisch rechnen und Definitionen (z.B. Was ist Osmose?) wiedergeben können. PC 2 besteht aus ca. 6 Aufgaben samt Unteraufgaben, in denen du sowohl rechnen als auch Diagramme zeichnen können musst (z.B. potenzielle Energie, siehe Beispielabbildung zu Katalyse). Die zur Verfügung stehende Bearbeitungszeit ist vorallem bei PC 2 tendenziell eher knapp.
Auf der letzten Seite gibt es eine angehängte Formelsammlung. Allerdings ist diese weder geordnet noch benötigst du alle Formeln, die dort drauf stehen. Zum Teil musst du die Formeln auch erst noch umstellen.
Empfehlung 1: Genügend Zeit investieren
Investiere viel Zeit in die Vor- und Nachbereitung der Vorlesung und Übung. Dann hast du es später, wenn es auf die Klausurvorbereitung zu geht deutlich leichter.
Wieviel Zeit sollte ich investieren? Solltest du keine Übungsgruppe haben, solltest du dich, spätestens am Tag vor der Übung intensiv mit den Aufgaben beschäftigen, damit sie dir auch noch am nächsten Tag präsent sind und du einen Ansatz hast, wie du an die Aufgabe herangehen würdest. Wieviel Zeit genau das in Anspruch nimmt, hängt von der Aufgabe ab, das können mal 10 Minuten sein und mal 1 – 2 Stunden. Ähnlich viel Zeit benötigst du in der Übungsgruppe.
Empfehlung 2: Zusätzliche Übungsaufgaben suchen und erstellen

Suche dir selbst Aufgaben zur Vorbereitung auf die Klausur raus und gehe nicht nur die Übungsaufgaben nochmal durch, denn das reicht oft nicht. Je mehr Variation du in den Aufgaben hast, desto besser verstehst du das Thema.
Du kannst dafür z.B. den Chemie-Fachschaftsrat (FSR) nach Altklausuren fragen und diese durchrechnen und mit Kommilitonen/innen vergleichen. Klausuren anderer Universitäten sind nicht immer hilfreich, da hier teilweise ein anderes Formelwissen vorausgesetzt wird.
Es kann auch helfen, wenn du eigene Aufgaben erstellst und Aufgaben, die von Kommilitonen/innen erstellt wurden berechnest. Dadurch verstehst du den Stoff besser. Du kannst dich dabei an den Übungsaufgaben orientieren und versuchen, diese abzuwandeln.
Empfehlung 3: (Digitale) Karteikarten erstellen und tauschen

Für Definitionen eigenen sich sehr gut Karteikarten. Entweder erstellt du diese handschriftlich oder du nutzt ein Softwareangebot wie zum Beispiel studysmarter oder Anki-cards. Tausche dich mit Kommilitonen/innen aus und fragt euch gegenseitig ab. Ein Tutorial, in dem erklärt wird, wie man mit Ankis lernt findest Du hier: Lernen mit Ankis.
Empfehlung 4: Beginne mit den für dich einfachen Aufgaben
In der Klausur solltest du mit den Aufgaben beginnen, bei denen du direkt ein Ansatz im Kopf hast oder weißt, welche Formel du benutzen musst, um die Aufgabe zu lösen. Den schwierigeren Aufgaben solltest du dich widmen, wenn du noch Zeit übrig hast.
Überlege dir, welche Formel du für die Aufgabe benötigst und prüfe, ob du einer der Formeln aus der angehängten Formelsammlung nutzen kannst. Oft bringen auch Ansätze schon Punkte, selbst wenn das Ergebnis nicht ganz richtig ist oder die Aufgabe nicht zu Ende bearbeitet wurde. Achte unbedingt darauf, dass du die geforderten Einheiten nutzt und das Ergebnis in der richtigen Einheit angibst. Es wird in der Klausur auch viel Wert daraufgelegt, dass du die „signifikanten Stellen“ berücksichtigst, ansonsten werden dir schnell wichtige Punkte abgezogen.


Aufgaben bearbeiten in 9 Schritten
Grundsätzlich empfehlen wir dir, an die Aufgaben der Übung – und später auch die der Klausur – wie folgt heran zu gehen. Sieh dir dazu unser Beispiel an.
Beispielaufgabe
![]() bei
bei ![]() und
und ![]() bei
bei ![]() werden bei
werden bei ![]() gemischt, wobei das Gesamtvolumen konstant bleibt. Berechnen Sie die Freie Mischungsenthalpie
gemischt, wobei das Gesamtvolumen konstant bleibt. Berechnen Sie die Freie Mischungsenthalpie ![]() .
.
Erstelle dir zunächst eine Übersicht aller gegebenen Werte, damit du später schneller siehst, welche dir bei der Endformel noch fehlen. Hier solltest du auch gleich die benötigten Einheiten berechnen, wie in diesem Fall Megapascal ![]() zu Pascal
zu Pascal ![]() oder Celsius zu Kelvin.
oder Celsius zu Kelvin.
![]()
![]()
![]()
![]()
![]()
Mache dir klar, was genau am Ende gesucht ist.
Freie Mischungsenthalpie ![]() .
.
Sieh in der Vorlesung oder zur Not im Internet nach, ob du eine geeignete Formel für das Gesuchte findest oder eine bekannte Formel umstellen kannst. Falls dir nichts einfällt, frage deine Kommilitonen oder deinen Übungsleiter/in bzw. Professor/in.
![]()
Überlege dir, welche Werte gegeben sind und welche dir noch fehlen und schreibe diese auf.
![]() = ?
= ?
![]() = ?
= ?
- Suche dir die Formel(n) für die Werte heraus, die dir noch fehlen. In diesem Fall die Formeln für
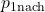 und
und 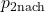 . Du wirst feststellen, dass du ggf. weitere Werte bzw. Formeln benötigst. In diesem Fall z.B. die Formel für
. Du wirst feststellen, dass du ggf. weitere Werte bzw. Formeln benötigst. In diesem Fall z.B. die Formel für  .
. - Suche diese Formel heraus und arbeite dich bis zu der Formel vor, in der du bekannte Werte einsetzen kannst, wie hier bei dem Volumen
- Setze diesen Wert wiederum in die vorherige Formel ein und arbeite dich so wieder zurück
- Achte zwischendurch immer wieder auf die richtigen Einheiten und signifikante Stellen
Beispiel zu Schritt 5&6:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Wie im Beispiel Pascal (Pa) zu Bar.
Nun kannst du die Zwischenergebnisse mit den richtigen Einheiten in die „Endformel“ einsetzen. Achte dabei unbedingt auf die signifikanten Stellen.
![]()
Am Beispiel aus Schritt 5 (Volumen berechnen): Meistens musst du zwischendurch und auch am Ende Einheiten umrechnen bzw. kürzen, sodass die richtige SI-Einheit rauskommt.
Zum Beispiel bei der Formel zur Volumenberechnung. Laut SI-Einheit soll das Volumen in ![]() angegeben werden.
angegeben werden.
Dafür musst du die Einheiten Joule (![]() ) und Pascal (
) und Pascal (![]() ) umrechnen (Kelvin und Mol kürzen sich in diesem Fall einfach weg). Rechnet man Joule und Pascal um, sieht man, wie sich das Gewicht (
) umrechnen (Kelvin und Mol kürzen sich in diesem Fall einfach weg). Rechnet man Joule und Pascal um, sieht man, wie sich das Gewicht (![]() ) und die Zeit (
) und die Zeit (![]() ) kürzen und
) kürzen und ![]() übrigbleibt.
übrigbleibt.
![]()
![]()
![]()
![]()
![]()
Am Ende rechnest du alles zusammen und schreibst das Ergebnis auf. Achte dabei zum einen auf die richtige Einheit – in diesem Fall musst du noch Joule zu Kilojoule umrechnen – zum anderen wieder auf die signifikanten Stellen. Aus der Formel von Schritt 7 erkennt man, dass das Ergebnis eine signifikante Stelle haben muss.
![]()
Einheit: ![]()
Signifikante Stellen: 2
![]()




Schreibe einen Kommentar